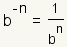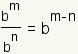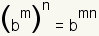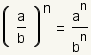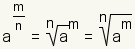Exponent
Pronunciation: /ˈɛks.poʊ.nənt/ ExplainAn exponent is used to indicate repeated multiplication, which is also called raising a base to a power. For example, 22 means base 2 raised to the power of 2 or 2 multiplied by itself 2 times: 2·2 = 4. 34 means 3·3·3·3 = 81. The process of raising a base to an exponent is called exponentiation.
An exponent can also be called a power. In British english, an exponent is called an index (plural indices).
A value with an exponent that is a unit fraction is called a
root or a
radical.
A special notation is used for roots. The base of the
expression is placed inside of a radical sign: 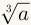
A negative exponent is used to indicate multiplication by a reciprocal (or multiplicative inverse), which is equivalent to division. So 2-3 = 1/(23) = 1/8.
Properties of Exponents
The properties of exponents can be derived from the definition of exponent.
| Property | Explanation |
|---|---|
| bm · bn = bm + n | As an example, let m = 2 and
n = 3.
Then bm = b2 = b · b,
and
bn = b3 = b · b · b.
So
bm · bn
= b2 · b3
Since there are five b's multiplied together,
b2 · b3 =
(b · b) · (b · b · b) = b5
|
| Mathematicians use a negative exponent to mean division, or to mean the reciprocal of a number. |
|
This says that when we use a negative exponent, we mean the multiplicative inverse, or reciprocal. To see how that works, look at the expression 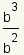 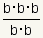 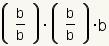 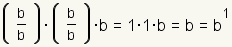 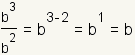 |
| To see why this is true, we will start with the right-hand side of the identity, 1. Start with the fact than any number divided by itself is 1, except for 0. So, 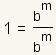    |
|
| Here, it is important to note that  This concept is an extension of the property that bm · bn = bm + n. However, we are dealing with repeated multiplication in both steps. Let's start with bm. Let m = 3. Then, b3 = b · b
· b
But, if n = 2, then
(b3)2 =
b3 · b3
Because the second exponent n = 2 mean
multiply b3 by itself twice. So,
(b3)2 =
b3 · b3 = (b
· b · b) · (b ·
b · b)
So,
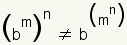 |
(ab)n = an · bn | Exponentiation distributes across multiplication. |
| Exponentiation distributes across division. |
| The numerator of a fractional exponent is a power. The denominator is a root. |
References
- McAdams, David E.. All Math Words Dictionary, exponent. 2nd Classroom edition 20150108-4799968. pg 76. Life is a Story Problem LLC. January 8, 2015. Buy the book
Cite this article as:
McAdams, David E. Exponent. 4/20/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. http://www.allmathwords.org/en/e/exponent.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
4/20/2019: Updated expressions and equations to match new format. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
7/5/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
2/2/2010: Added "References". (McAdams, David E.)
2/10/2009: Added fractional exponent. (McAdams, David E.)
1/9/2009: Added distributive properties of exponentiation. (McAdams, David E.)
1/4/2009: Added 'More Information'. (McAdams, David E.)
11/25/2008: Changed equations to images. (McAdams, David E.)
2/4/2008: Correct typographical errors. (McAdams, David E.)
8/7/2007: Initial Version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License